Self-evaluation test
The following 40 multiple-choice questions give a representative overview what the actual Admission test will be like.Basic mathematics
What is logk(10k)?
- k*logk(10)
- 10
- k/10
- k*log10(k)
What is (100k)1/2?
- 1/10k
- 10k
- 50k
- k50
What is k-1/2 (for k > 0)?
- 1/k0.5
- -k0.5
- k2
- 21/k
log(m+n) = log(m) * log(n). Is this statement true or false (for both m and n > 0)?
- True
- False
Below you find the matrices M1 and M2. What is their matrix product, i.e. what is M1T * M2?
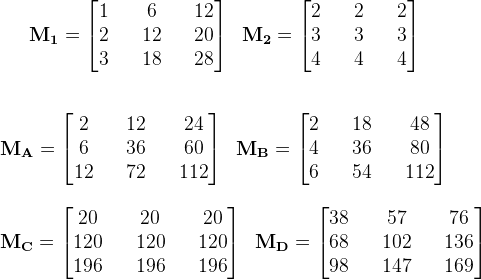
- MA
- MB
- MC
- MD
Which vector is orthogonal to v (i.e. forms a 90 degree angle with it)?
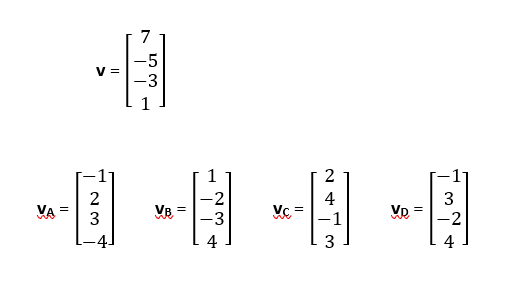
- vA
- vB
- vC
- vD
What is the derivative of f(x) = log(x1/2 + 2) (with respect to x)?
- x1/2 / (2x1/2 + 4)
- -1 / (2x + 4x1/2)
- -x1/2 / (2x1/2 + 4)
- 1 / (2x + 4x1/2)
What is the integral of f(x) = xe2x (with respect to x)?
- (2x - 1)ex / 2 + Constant
- (2x - 1)e2x / 2 + Constant
- (2x - 1)ex / 4 + Constant
- (2x - 1)e2x / 4 + Constant
At what value does the function f(x) = -4x2 + 16x reach a maximum?
- -8
- 0
- 2
- None of the other options: the function f(x) reaches a minimum.
What is the area under the curve f(x) = 6x2 between the values x=-2 and x=2?
- 0
- 16
- 32
- 48
Probability
If two fair dice are thrown at the same time, then what is the probability that a 1 is thrown first and a 2 next?
- 1/36
- 1/18
- 1/6
- 1/3
A letter is chosen at random from the word PROBABILITY. What is the probability that it is the letter B or I?
- 4/11
- 2/11
- 1/4
- 1/2
If a family has three children, then what is the probability that the family has AT LEAST two boys? Assume that a child of either gender is equally likely.
- 3/8
- 1/3
- 1/2
- 2/3
If three fair coins are thrown at the same time, then what is the probability of not obtaining three tails?
- 1/3
- 2/3
- 7/8
- 8/8
A company with 60 % male employees has 30 % female employees who work part-time. What is the probability that an employee of the company works part-time given it is a female employee?
- 3/4
- 12/100
- 3/10
- 4/10
If a family has two children, then what is the probability that both of them are girls given that AT LEAST one of them is a girl? Assume that a child of either gender is equally likely.
- 3/8
- 1/3
- 1/2
- 2/3
If a card is randomly drawn from a standard pack of 52 playing cards, then what is the probability of getting a diamond or an ace?
- 1/52
- 4/13
- 5/13
- 17/52
If two fair six-sided dice are thrown at the same time, what is the probability that the sum of the faces showing up is 7?
- 1/9
- 1/12
- 1/6
- 1/4
One bag of 200 marbles has 20% red marbles, 50% blue marbles and 30% green marbles. Another bag of 100 marbles has 20% red marbles, 10% blue marbles and 70% green marbles. Both bags are mixed and a blue marble is randomly drawn from the mix. What is the probability that it came from the first bag?
- 1/11
- 1/2
- 3/5
- 10/11
Given the following probabilities (in percentages) for the ordinal variable X, what is the probability of X smaller than or equal to 1?
| X | Percentage |
| 0 | 1 |
| 1 | 3 |
| 2 | 24 |
| 3 | 34 |
| 4 | 26 |
| 5 | 12 |
- 1/100
- 3/100
- 1/25
- 1/75
Statistics
Consider the data values 10, 5, 6, 17, 13, 9, 19, 14, 7, 9. Their sample mean with 10 % of the values trimmed is 11.250.
- True
- False
Consider the following graph. It shows that the variance of the data is about 5.
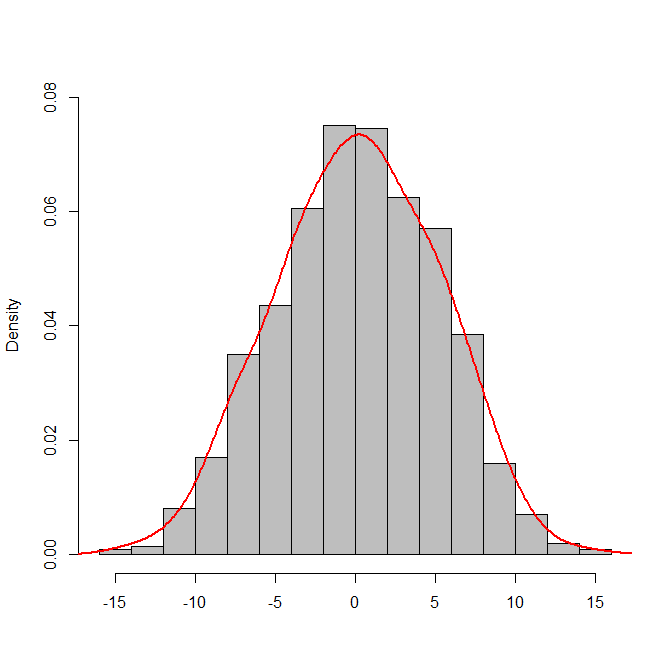
- True
- False
Consider the following boxplot (of values drawn from a chi-squared distribution with 1 degree of freedom). It shows that the data values are left-skewed, so the mean is probably bigger than the median.
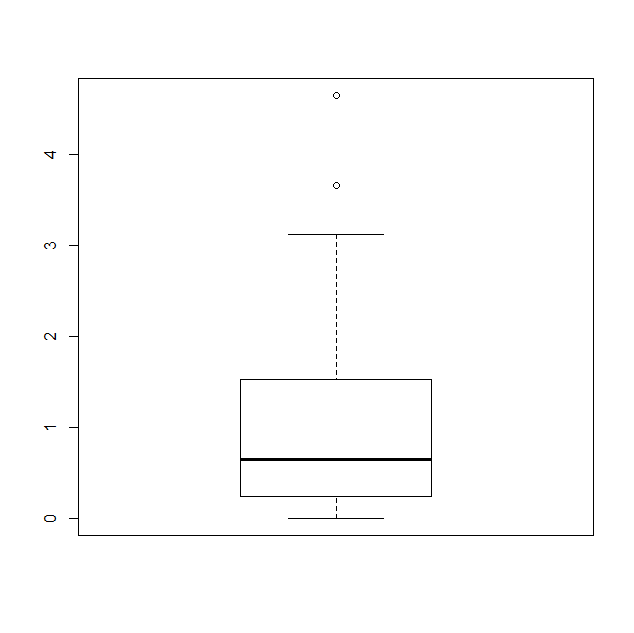
- True
- False
The covariance of two standardized variables is always equal to their (Pearson's) correlation.
- True
- False
A low p-value suggests that the null hypothesis is true.
- True
- False
Suppose researchers set up a study to evaluate a new treatment for allergies. Beforehand they specify that the chance of erroneously missing an effect equals 15%, while the chance of erroneously finding an effect equals 10%. When the eventual analysis returns a p-value of 0.12, the researchers will not reject the null hypothesis.
- True
- False
If you falsely do not reject the null hypothesis in a statistical hypothesis test, then you have a so-called significant result.
- True
- False
Consider a one-sample t-test for H0: μ = 0. For a lower sample average but with the same sample size and sample variance the p-value can be expected to decrease.
- True
- False
Consider the chi-square test for a frequency table. Its null hypothesis implies that the distribution across the columns depends on the rows.
- True
- False
A farmer compares two fertilizing methods by means of a t-test. The 95 % confidence interval of the difference in mean yield between both methods is [-50; 850] euro. This implies that the difference in mean yield in this specific study is 400 euro.
- True
- False
R programming
The function load() loads a package in R and the function help() opens a help page.
- False for load() and false for help()
- False for load() but true for help()
- True for load() but false for help()
- True for load() and true for help()
Consider a vector x with 100 values in R. The command x[x == 50] selects those elements in x which are equal to 50 and the command x[-99] selects the one but last element in x.
- False for x[x == 50] and false for x[-99]
- True for x[x == 50] but false for x[-99]
- False for x[x == 50] but true for x[-99]
- True for x[x == 50] and true for x[-99]
With which R commands do you create the vectors [3, 2, 1,…, 3, 2, 1] and [5, 5, 5,…, 9, 9, 9] (each of length 15)?
- rep(3:1, times = 5) and rep(5:9, each = 3)
- rep(3:1, each = 5) and rep(5:9, times = 3)
Which R command implements the following mathematical expression (considering that the xi values are stored in a vector x of length N)?
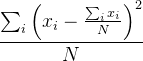
- sum((x – sum(x)/len(x))^2) / len(x)
- sum((x – sum(x)/length(x))^2) / length(x)
- summate((x – summate(x)/len(x))^2) / len(x)
- summate((x – summate(x)/length(x))^2) / length(x)
The command for (i in 1:(length(x) - 1)) { x[i] <- x[i] + x[i + 1] } does the same as the function cumsum() and the command while (sum(y) < 10) { y <- y * 2 } will double each element in y (you can assume that x and y are existing objects in R).
- False for the for command and false for the while command
- True for the for command and true for the while command
- False for the for command but true for the while command
- True for the for command but false for the while command
If mat is a 100x100 matrix, and both vec1 and vec2 are vectors of 100 elements, then the commands rbind(cbind(mat, vec1), vec2) and cbind(cbind(mat, vec1), vec2) will produce a 101x101 matrix.
- False for rbind(cbind(mat, vec1), vec2) and false for cbind(cbind(mat, vec1), vec2)
- True for rbind(cbind(mat, vec1), vec2) and true for cbind(cbind(mat, vec1), vec2)
- True for rbind(cbind(mat, vec1), vec2) but false for cbind(cbind(mat, vec1), vec2)
- False for rbind(cbind(mat, vec1), vec2) but true for cbind(cbind(mat, vec1), vec2)
The R function average() computes the statistical average of a vector and the function mode() computes its statistical mode.
- False for average() and false for mode()
- False for average() but true for mode()
- True for average() but false for mode()
- True for average() and true for mode()
Consider a numeric vector y in R and a grouping vector x (both of the same length). You can do a two-sided t-test with the R command t.test(y ~ x) and you can access its p-value with the command t.test(y ~ x)@p.value.
- False for t.test(y ~ x) and false for t.test(y ~ x)@p.value
- False for t.test(y ~ x) but true for t.test(y ~ x)@p.value
- True for t.test(y ~ x) but false for t.test(y ~ x)@p.value
- True for t.test(y ~ x) and true for t.test(y ~ x)@p.value
The function tr() generates t-distributed random values in R and the function fd() gives the probability under an F-distribution.
- False for tr() and false for fd()
- False for tr() but true for fd()
- True for tr() but false for fd()
- True for tr() and true for fd()
Which function in R is a high-level plotting function (i.e. it creates a new plot) and which is a low-level plotting function (i.e. it adds information to an existing plot)?
- High-level: text(), low-level: title()
- High-level: hist(), low-level: title()
- High-level: hist(), low-level: barplot()
- High-level: barplot(), low-level: hist()
Scores
Since the Admission test consists of multiple-choice questions, it is marked according to Ghent University's regulations on multiple-choice tests. In addition, you need to correctly answer at least half of the questions in each of the four subsections (i.e. Basic mathematics, Probability, Statistics and R programming). Finally, you need to complete the test within 70 minutes.The correct answers to the questions above are:
- k*logk(10)
- 10k
- 1/k0.5
- False
- MC
- vC
- 1 / (2x + 4x1/2)
- (2x - 1)e2x / 4 + Constant
- 2
- 32
- 1/36
- 4/11
- 1/2
- 7/8
- 3/4
- 1/3
- 4/13
- 1/6
- 10/11
- 1/25
- False
- False
- False
- True
- False
- True
- False
- False
- False
- True
- False for load() but true for help()
- True for x[x == 50] but false for x[-99]
- rep(3:1, times = 5) and rep(5:9, each = 3)
- sum((x – sum(x)/length(x))^2) / length(x)
- False for the for command and false for the while command
- False for rbind(cbind(mat, vec1), vec2) and false for cbind(cbind(mat, vec1), vec2)
- False for average() and false for mode()
- True for t.test(y ~ x) but false for t.test(y ~ x)@p.value
- False for tr() and false for fd()
- High-level: hist(), low-level: title()